Dopocitej.cz - Přejít na úvodní stránku

JEHLAN PRAVIDELNÝ VICEBOKÝ:

VÝPOČET POVRCHU, POVRCHU PLÁŠTĚ, OBJEMU, POVRCHOVÉ PŘÍČKY, VÝŠKY, DÉLEK STRAN, POČET STRAN A POLOMĚRU PODSTAVY PRAVIDELNÉHO VÍCEBOKÉHO JEHLANU ZE VZTAHŮ:



Geometrické znázornění pravidelného vícebokého jehlanu s vyznačennou délkou hrany, výškou, výškou na hranu a polomerem kružnice opsané podstavě
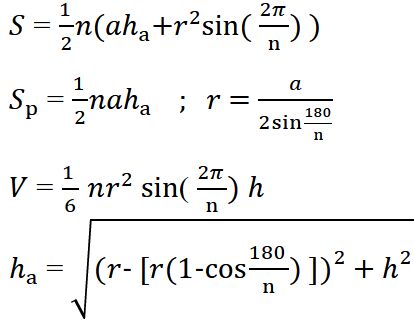Vzorce pro výpočet obsahu povrchu, povrchu pláště, výšky na hranu a objemu pravidelného více bokého hranolu


TIP: pokud máte zadanou jinou veličinu k výpočtu pravidelného vícebokého jehlanu, můžete ji dopočítat ze vztahů pro pravidelný mnohoúhelník nebo pravoúhlý trojúhelník

Zadejte jakékoliv tři veličiny a zvolte všechny jednotky
VÝSLEDKY
Délka strany a =
Počet stran n =
Výška jehlanu h =
Výška na stranu a ha =
Poloměr opsané kružnice r =
Povrch jehlanu S =
Povrch pláště jehlanu Sp =
Objem jehlanu V =
a
n
h
ha
r
S
Sp
V


pozn.: výsledné hodnoty jsou zaokrouhlovány na tři desetinná místa
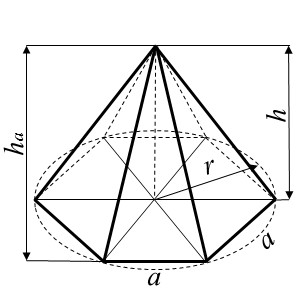
Definice pravidelného vícebokého jehlanu

Definice pravidelného vícebokého jehlanu

Pravidelný víceboký jehlan je těleso, jehož podstavou je pravidelný n-úhelník (např. trojúhelník, čtverec, pětiúhelník, šestiúhelník, atd.) a jehož vrchol leží nad středem podstavy.

  • Má n bočních stěn ve tvaru shodných rovnoramenných trojúhelníků.
  • Všechny boční hrany mají stejnou délku.
  • Osa jehlanu je kolmá k rovině podstavy a prochází jejím středem i vrcholem jehlanu.
  • Je to prostorové těleso s (n + 1) stěnami, 2n hranami a (n + 1) vrcholy.
Výška pravidelného vícebokého jehlanu

Výška pravidelného vícebokého jehlanu

Výška (v) je kolmá vzdálenost mezi vrcholem jehlanu a rovinou podstavy. Výška spojuje vrchol jehlanu se středem podstavy.

Pokud známe délku boční hrany b a poloměr kružnice vepsané podstavě r, pak platí:

  • v = √(b² - r²)
Objem pravidelného vícebokého jehlanu

Objem pravidelného vícebokého jehlanu

Objem (V) pravidelného vícebokého jehlanu se vypočítá podle vzorce:

  • V = (1/3) · Sp · v

kde:

  • Sp – obsah pravidelné n-úhelníkové podstavy,
  • v – výška jehlanu.

Obsah podstavy lze vyjádřit pomocí délky strany a a počtu stran n:

  • Sp = (n · a²) / (4 · tan(π/n))
Povrch pravidelného vícebokého jehlanu

Povrch pravidelného vícebokého jehlanu

Povrch (S) pravidelného vícebokého jehlanu tvoří podstava a boční plášť složený z n shodných rovnoramenných trojúhelníků:

  • S = Sp + Spláště

nebo podrobněji:

  • S = (n · a²) / (4 · tan(π/n)) + (n · a · s) / 2

kde s je výška boční stěny (výška bočního trojúhelníka).

Povrch pláště pravidelného vícebokého jehlanu

Povrch pláště pravidelného vícebokého jehlanu

Povrch pláště (Spláště) se skládá z n shodných rovnoramenných trojúhelníků, jejichž základnou je strana podstavy a a výškou s (výška boční stěny):

  • Spláště = (n · a · s) / 2

Výšku boční stěny s lze vypočítat pomocí výšky jehlanu v a poloměru kružnice vepsané podstavě r:

  • s = √(v² + r²)
Výška na hranu podstavy

Výška na hranu podstavy

Výška na hranu podstavy (vh) je výška boční trojúhelníkové stěny vedená z vrcholu jehlanu kolmo na hranu podstavy.

  • vh = √(v² + (a/2 · tan(π/n))²)

Tato výška je shodná s výškou bočního trojúhelníka.

Zajímavosti o pravidelném vícebokém jehlanu

Zajímavosti o pravidelném vícebokém jehlanu

  • Jehlan se používá při modelování střech, pyramid a architektonických konstrukcí.
  • Při n = 3 získáme pravidelný trojboký jehlan (čtyřstěn).
  • Při n = 4 jde o pravidelný čtyřboký jehlan.
  • Pro velké n se tvar jehlanu blíží kuželu.
  • Jehlany se často používají i při výpočtech objemu střech a kuželovitých konstrukcí.