MNOHOÚHELNÍK
MNOHOÚHELNÍK - PRAVIDELNÝ:
VÝPOČET OBSAHU, OBVODU, STRANY, ÚHLU, KRUŽNICE VEPSANÉ A OPSANÉ PRAVIDELNÉHO MNOHOÚHELNÍKU ZE VZTAHŮ:
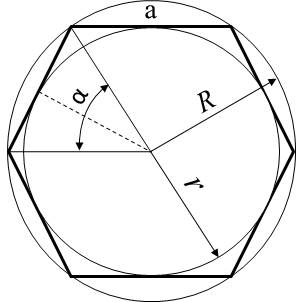 |
 |
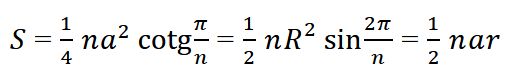 |
|
MNOHOÚHELNÍK
 |
 |
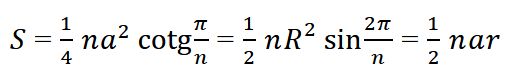 |
|
Definice pravidelného mnohoúhelníku
Definice pravidelného mnohoúhelníku
Pravidelný mnohoúhelník je rovinný geometrický útvar, který má:
Označuje se jako n-úhelník, kde n je počet jeho stran. Pokud je n = 3, jde o rovnostranný trojúhelník; pokud n = 4, jde o čtverec; pro vyšší hodnoty vznikají pravidelné pětiúhelníky, šestiúhelníky apod.
Obvod pravidelného mnohoúhelníku
Obvod pravidelného mnohoúhelníku
Obvod (O) pravidelného n-úhelníku se vypočítá podle vzorce:
O = n · a
kde n je počet stran a a je délka jedné strany. Tento vztah je přímý, protože všechny strany jsou shodné.
Obsah pravidelného mnohoúhelníku
Obsah pravidelného mnohoúhelníku
Obsah (S) pravidelného n-úhelníku se dá vyjádřit několika způsoby, nejčastěji:
Tento vzorec vychází z rozdělení mnohoúhelníku na n shodných rovnoramenných trojúhelníků.
Poloměr kružnice opsané pravidelnému mnohoúhelníku
Poloměr kružnice opsané pravidelnému mnohoúhelníku
Poloměr kružnice opsané (ro) vyjadřuje vzdálenost středu mnohoúhelníku od jeho vrcholů. Vypočítá se podle vztahu:
ro = a / (2 · sin(π / n))
Všechny vrcholy pravidelného mnohoúhelníku leží právě na této kružnici.
Poloměr kružnice vepsané pravidelnému mnohoúhelníku
Poloměr kružnice vepsané pravidelnému mnohoúhelníku
Poloměr kružnice vepsané (rv) určuje vzdálenost středu mnohoúhelníku od jeho stran. Lze jej vypočítat podle vzorce:
rv = a / (2 · tan(π / n))
Vepsaná kružnice se dotýká všech stran mnohoúhelníku a její střed se shoduje se středem kružnice opsané.
Zajímavosti o pravidelném mnohoúhelníku
Zajímavosti o pravidelném mnohoúhelníku