Jak vypočítat přeponu pravoúhlého trojúhelníku?

Přeponu c vypočítáte z Pythagorovy věty: c = √(a² + b²).

Jak vypočítat obsah pravoúhlého trojúhelníku?

Obsah se určí jednoduše podle vzorce S = (a × b) / 2, kde a a b jsou odvěsny.

Jak zjistit výšku na přeponu?

Výšku na přeponu spočítáte ze vztahu v_c = (a × b) / c.

Jak vypočítat úhly pravoúhlého trojúhelníku?

Pomocí goniometrických funkcí: α = arcsin(a / c), β = arccos(a / c), přičemž α + β = 90°.

Jaký je poloměr opsané a vepsané kružnice pravoúhlého trojúhelníku?

Opsaná kružnice má poloměr R = c / 2 (střed je uprostřed přepony). Vepsaná kružnice má poloměr r = (a + b − c) / 2.

TROJÚHELNÍK - PRAVOÚHLÝ

TROJÚHELNÍK - PRAVOÚHLÝ:

VÝPOČET OBSAHU, OBVODU, STRAN, ÚHLŮ, VÝŠKY PRAVOÚHLÉHO TROJÚHELNÍKU A POLOMĚRU KRUŽNIC TROJÚHELNÍKU VEPSANÉ A OPSANÉ ZE VZTAHŮ:

Geometrické znázornění pravoúhlého trojúhelniku s vyznačeným poloměrem kručnice opsané a vepsané, stranami, úhly a výškou

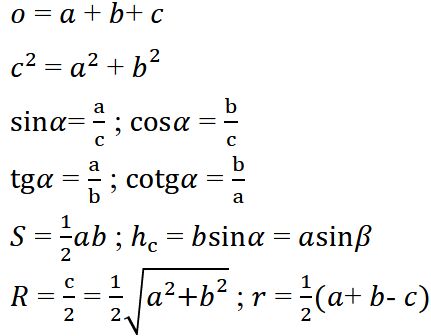Vzorce pro obvod, obsah, polomery kružnic vepsané a opsané a strany pravoúhlého trojúhelníku

Zadejte jakoukoliv dvě veličiny a zvolte všechny jednotky

VÝSLEDKY

Délka strany trojúhelníku a =
Délka strany trojúhelníku b =
Délka strany trojúhelníku c =
Uhel α =		°
Uhel β =		°
Výška trojúhelníku na stranu c h_c =
Pol. kružnice trojúhel. vepsaná r =
Pol. kružnice trojúhel. opsaná R =
Obsah trojúhelníku S =
Obvod trojúhelníku O =

a
b
c
α		°
β		°
h_c
r
R
S
O

pozn.: výsledné hodnoty jsou zaokrouhlovány na tři desetinná místa

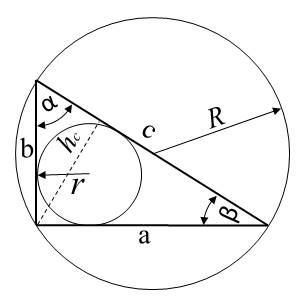
Definice pravoúhlého trojúhelníku

Pravoúhlý trojúhelník je trojúhelník, který má jeden vnitřní úhel pravý (90°).

Strana naproti pravému úhlu se nazývá přepona (c).
Zbývající dvě strany se nazývají odvěsny (a, b).
Součet všech vnitřních úhlů je 180°.

Pravoúhlý trojúhelník je základním útvarem v geometrii, trigonometrických funkcích i technické praxi.

Pythagorova věta

Pro pravoúhlý trojúhelník platí základní vztah mezi stranami:

c² = a² + b²

Tento vztah vyjadřuje, že čtverec nad přeponou se rovná součtu čtverců nad odvěsnami. Slouží k výpočtu délek stran i při určení vzdáleností v rovině nebo prostoru.

Obvod pravoúhlého trojúhelníku

Obvod (O) se vypočítá jako součet všech tří stran:

O = a + b + c

Pokud známe délky odvěsen, lze přeponu určit z Pythagorovy věty a následně dopočítat obvod.

Obsah pravoúhlého trojúhelníku

Obsah (S) se vypočítá jednoduše jako:

S = (a · b) / 2

kde a a b jsou odvěsny. Tento vztah vychází z faktu, že pravoúhlý trojúhelník je polovinou obdélníka o stranách a a b.

Výšky pravoúhlého trojúhelníku

Pravoúhlý trojúhelník má tři výšky, z nichž jedna leží přímo na přeponě (je totožná s pravým úhlem).

Výška na přeponu (v_c) se dá vypočítat jako:

v_c = (a · b) / c

Každá výška rozděluje trojúhelník na dva menší pravoúhlé trojúhelníky podobné původnímu.

Poloměr kružnice vepsané pravoúhlému trojúhelníku

Poloměr kružnice vepsané (r_v) se vypočítá podle vztahu:

r_v = (a + b - c) / 2

Střed kružnice leží uvnitř trojúhelníku a kružnice se dotýká všech tří jeho stran.

Poloměr kružnice opsané pravoúhlému trojúhelníku

Poloměr kružnice opsané (r_o) se rovná polovině délky přepony:

r_o = c / 2

Střed kružnice leží přesně ve středu přepony, což je zvláštní vlastnost pravoúhlých trojúhelníků.

Zajímavosti o pravoúhlém trojúhelníku

Je základem trigonometrie – definují se na něm funkce sinus, kosinus a tangens.
V pravoúhlém trojúhelníku platí Pythagorova věta, jedna z nejznámějších v celé matematice.
Speciálním případem je rovnoramenný pravoúhlý trojúhelník, kde a = b a úhly jsou 45°, 45°, 90°.
Pravoúhlé trojúhelníky se hojně používají v stavebnictví, fyzice a kartografii.
Jejich vlastnosti umožňují přesné výpočty výšek, vzdáleností a sklonů pomocí jednoduchých vzorců.