KRUHOVÝ OBLOUK:

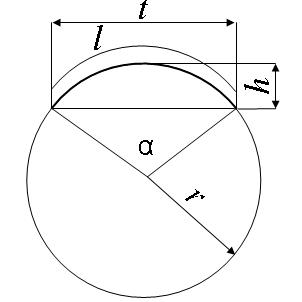
VÝPOČET POLOMĚRU, ÚHLU, DÉLKY OBLOUKU, VÝŠKY OBLOKU A DÉLKY TĚTIVY KRUHOVÉHO OBLOUKU ZE VZTAHŮ:


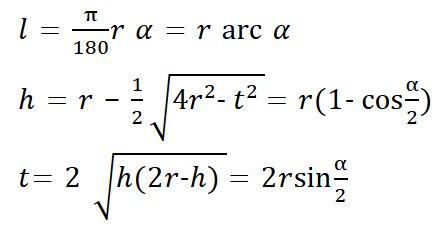TIP: pokud máte zadanou jinou veličinu k výpočtu kruhového oblouku můžete ji dopočítat ze vztahů pro kruh

Zadejte jakékoliv dvě veličiny a zvolte všechny jednotky
VÝSLEDKY
Poloměr kružnice r =
Uhel  α = °
Délka obouku l =
Výška obouku h =
Délka tětivy t =
r
α
°
l
h
t


pozn.: výsledné hodnoty jsou zaokrouhlovány na tři desetinná místa