Jak vypočítat objem pravidelného vícebokého komolého jehlanu?

Objem se vypočítá pomocí vzorce V = (v/3) × (S₁ + S₂ + √(S₁ × S₂)), kde v je výška a S₁ a S₂ jsou obsahy spodní a horní podstavy.

Jaký je povrch pravidelného n-bokého komolého jehlanu?

Povrch je součtem obsahů obou podstav a pláště tvořeného n rovnoramennými lichoběžníky.

Jak se počítá sklopená výška komolého jehlanu?

Sklopená výška vₛ se určí jako výška rovnoramenného lichoběžníku tvořícího boční stěnu: vₛ = √(s² − (R₁ − R₂)²).

Kolik má komolý jehlan hran, stěn a vrcholů?

Má 2n vrcholů, 3n hran a n + 2 stěny (2 podstavy a n bočních lichoběžníků).

Jaký je rozdíl mezi jehlanem a komolým jehlanem?

Komolý jehlan vznikne seříznutím vrcholu jehlanu rovinou rovnoběžnou s podstavou. Má dvě podstavy a lichoběžníkové boční stěny.

JEHLAN VÍCEBOKÝ KOMOLÝ

JEHLAN PRAVIDELNÝ VÍCEBOKÝ KOMOLÝ:

VÝPOČET POVRCHU, POVRCHU PLÁŠTĚ, OBJEMU, POVRCHOVÉ PŘÍČKY, VÝŠKY, DÉLEK STRAN, POČET STRAN A POLOMĚRU PODSTAV PRAVIDELNÉHO VÍCEBOKÉHO KOMOLÉHO JEHLANU ZE VZTAHŮ:

Pozor!

Zrejme mate vypnutou podporu JavaScriptu.

V tomto pripade vypocet nebude funkcní!!!

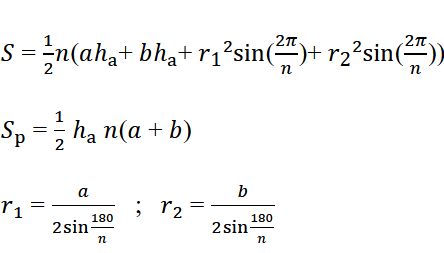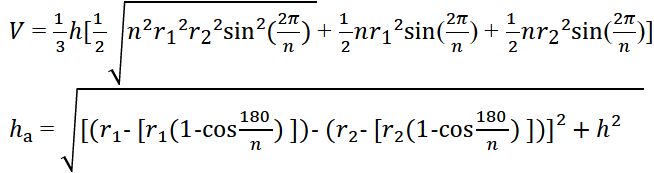TIP: pokud máte zadanou jinou veličinu k výpočtu pravidelného vícebokého komolého jehlanu, můžete ji dopočítat ze vztahů pro pravidelný mnohoúhelník nebo lichoběžník

Zadejte jakékoliv čtyři veličiny a zvolte všechny jednotky

VÝSLEDKY

Délka strany a =
Délka strany b =
Počet stran n =
Výška jehlanu h =
Výška na stranu a h_a =
Poloměr opsané kružnice r₁ =
Poloměr opsané kružnice r₂ =
Povrch komolého jehlanu S =
Povrch pláště kom. jehl. S_p =
Objem komolého jehlanu V =

a
b
n
h
h_a
r₁
r₂
S
S_p
V

pozn.: výsledné hodnoty jsou zaokrouhlovány na tři desetinná místa

Definice pravidelného vícebokého komolého jehlanu

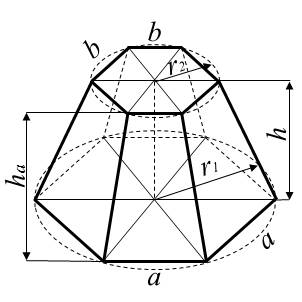
Pravidelný víceboký komolý jehlan vznikne tak, že původní pravidelný n-boký jehlan seřízneme rovinou rovnoběžnou s podstavou. Výsledkem jsou dvě podstavy – větší (spodní) a menší (horní) – obě jsou pravidelné n-úhelníky.

Má n shodných lichoběžníkových bočních stěn.
Horní podstava je zmenšenou podobou podstavy spodní.
Výška je kolmá vzdálenost mezi podstavami.
Je to těleso s (n + 2) stěnami, 3n hranami a 2n vrcholy.

Výška pravidelného vícebokého komolého jehlanu

Výška (v) je kolmá vzdálenost mezi rovnoběžnými podstavami.

Lze ji spočítat z výšky boční stěny s a rozdílu poloměrů kružnic vepsaných do podstav:

v = √(s² − (r₁ − r₂)²)

kde:

r₁ – poloměr kružnice vepsané spodní podstavě,
r₂ – poloměr kružnice vepsané horní podstavě.

Objem pravidelného vícebokého komolého jehlanu

Objem (V) komolého jehlanu určíme vzorcem:

V = (v / 3) · (S₁ + S₂ + √(S₁ · S₂))

kde:

S₁ – obsah spodní podstavy,
S₂ – obsah horní podstavy,
v – výška komolého jehlanu.

Obsah pravidelného n-úhelníka:

S = (n · a²) / (4 · tan(π/n))

Tento vzorec se použije pro obě podstavy zvlášť (s různými délkami stran a₁ a a₂).

Povrch pravidelného vícebokého komolého jehlanu

Celkový povrch (S) se skládá ze dvou pravidelných n-úhelníkových podstav a pláště:

S = S₁ + S₂ + S_pláště

Podstavy jako pravidelné n-úhelníky:

S₁ = (n · a₁²) / (4 · tan(π/n))
S₂ = (n · a₂²) / (4 · tan(π/n))

Povrch pláště pravidelného vícebokého komolého jehlanu

Boční plášť se skládá z n shodných lichoběžníků, každý se základnami a₁, a₂ a výškou lichoběžníku s (boční výškou):

S_pláště = n · (a₁ + a₂)/2 · s

Výška lichoběžníku (boční stěny) je:

s = √(v² + (r₁ − r₂)²)

Výška na hranu podstavy

Výška na hranu podstavy (v_h) je výška lichoběžníka vedená kolmo na hranu podstavy. U komolého jehlanu je tato výška shodná pro všechny lichoběžníky.

v_h = s

protože boční stěna je lichoběžník s výškou s.

Zajímavosti o pravidelném vícebokém komolém jehlanu

Při a₂ → 0 se komolý jehlan mění na běžný pravidelný n-boký jehlan.
Při velkém počtu stran n → ∞ se blíží komolému kuželu.
Geometricky se jedná o těleso vzniklé "ořezáním" vrcholu jehlanu.
Používá se v architektuře, modelování střech a při konstrukcích věží a altánů.
Je to jedno z nejčastěji využívaných těles při výpočtech objemů zemních prací.