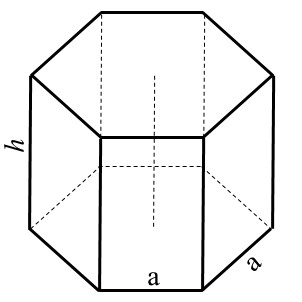
VÍCEBOKÝ HRANOL
VÍCEBOKÝ PRAVIDELNÝ HRANOL:
VÝPOČET POVRCHU, POVRCHU PLÁŠTĚ, OBJEMU, DÉLKY STRANY, POČTU STRAN A VÝŠKY PRAVIDELNÉHO VÍCEBOKÉHO HRANOLU ZE VZTAHŮ:
 |
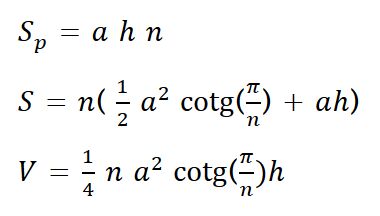 |
TIP:
pokud máte zadanou jinou veličinu k výpočtu hranolu, můžete ji dopočítat ze vztahů pro
pravidelný mnohouhelník


Definice pravidelného vícebokého hranolu
Definice pravidelného vícebokého hranolu
Pravidelný víceboký hranol je hranaté těleso, které má dvě rovnoběžné a shodné podstavy ve tvaru pravidelného n-úhelníku a n bočních stěn ve tvaru obdélníků (u kolmého hranolu) nebo rovnoběžníků (u šikmého hranolu).
Pokud jsou boční hrany kolmé k podstavám, jedná se o kolmý pravidelný hranol. Tento hranol může být trojboký, čtyřboký, pěti- nebo víceboký podle počtu stran podstavy (n).
Výška podstavy pravidelného vícebokého hranolu
Výška podstavy pravidelného vícebokého hranolu
Výška podstavy (va) je výška pravidelného n-úhelníku tvořícího podstavu hranolu.
U pravidelného n-úhelníku se dá určit pomocí poloměru vepsané kružnice (r) nebo pomocí délky strany a:
Tato výška se používá při výpočtu obsahu podstavy i celého hranolu.
Objem pravidelného vícebokého hranolu
Objem pravidelného vícebokého hranolu
Objem (V) pravidelného vícebokého hranolu je dán součinem obsahu podstavy a výšky hranolu:
Obsah pravidelného n-úhelníku s délkou strany a je:
Celkově tedy:
Povrch pravidelného vícebokého hranolu
Povrch pravidelného vícebokého hranolu
Povrch (S) je součet obsahů obou podstav a pláště:
kde Spláště je povrch pláště tvořeného n obdélníky. Pro kolmý pravidelný hranol se stranou podstavy a, výškou v a počtem stran n platí:
Povrch pláště pravidelného vícebokého hranolu
Povrch pláště pravidelného vícebokého hranolu
Povrch pláště (Spláště) je součet obsahů všech bočních stěn hranolu. Každá stěna je obdélník s délkou a a výškou v.
Tento povrch odpovídá ploše rozvinutého pláště hranolu, který tvoří obdélník s rozměry o = n · a (obvod podstavy) a v.
Úhlopříčka pravidelného vícebokého hranolu
Úhlopříčka pravidelného vícebokého hranolu
Úhlopříčka (u) spojuje dva vrcholy hranolu, které neleží v jedné podstavě. U kolmého hranolu závisí na délce úhlopříčky podstavy a výšce hranolu.
kde d je úhlopříčka pravidelného n-úhelníku. Pro šestiúhelník například platí d = 2a.
Zajímavosti o pravidelném vícebokém hranolu
Zajímavosti o pravidelném vícebokém hranolu