KOSODÉLNÍK
KOSODÉLNÍK:
VÝPOČET OBSAHU, OBVODU, STRAN, ÚHLOPŘÍČEK, ÚHLU A VÝŠKY KOSODÉLNÍKU, ROVNOBĚŽNÍKU ZE VZTAHŮ:
 |
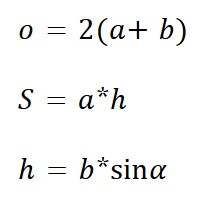 |
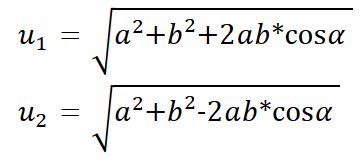 |
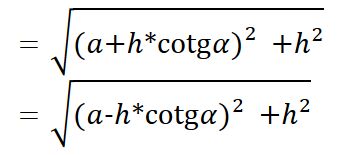 |
KOSODÉLNÍK
 |
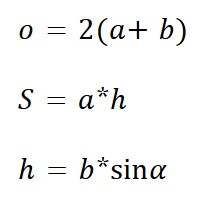 |
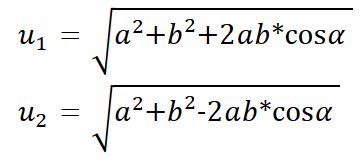 |
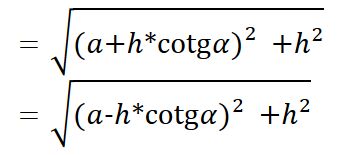 |
Definice kosodélníku
Definice kosodélníku
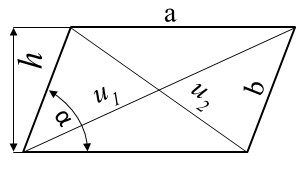
Kosodélník (paralelogram) je rovinný geometrický útvar patřící mezi čtyřúhelníky, který má:
Kosočtverec, obdélník i čtverec jsou speciálními případy kosodélníku.
Obsah kosodélníku
Obsah kosodélníku
(S) se nejčastěji počítá podle vzorce:Obsah kosodélníku je roven obsahu obdélníku se stejnou základnou a výškou.
Obvod kosodélníku
Obvod kosodélníku
(O) se vypočítá podle vzorce O = 2(a + b), kde a a b jsou délky sousedních stran. Tento vztah platí pro všechny kosodélníky, včetně obdélníku a kosočtverce.Úhlopříčky kosodélníku
Úhlopříčky kosodélníku
Úhlopříčky kosodélníku se navzájem půlí, ale obecně nejsou:Jejich délky lze vyjádřit pomocí stran a úhlu mezi nimi:
Úhlopříčky se protínají v bodě, který je středem souměrnosti kosodélníku.
Poloměr kružnice opsané kosodélníku
Poloměr kružnice opsané kosodélníku
Obecně kosodélník nemá opsanou kružnici, protože součet protilehlých úhlů není 180°. Výjimkou je obdélník (a tedy i čtverec), pro který opsaná kružnice existuje.
Poloměr kružnice vepsané kosodélníku
Poloměr kružnice vepsané kosodélníku
Vepsaná kružnice v kosodélníku existuje pouze tehdy, pokud je součet délek sousedních stran stejný, tedy a + b = c + d. Tato podmínka platí např. pro kosočtverec a čtverec.
Pokud kružnice existuje, její poloměr lze vypočítat jako: r = S / s, kde S je obsah a s je poloviční obvod.
Zajímavosti o kosodélníku
Zajímavosti o kosodélníku