KOSOČTVEREC
KOSOČTVEREC:
VÝPOČET OBSAHU, OBVODU, STRANY, ÚHLOPŘÍČEK, ÚHLU, VÝŠKY A KRUŽNICE VEPSANÉ KOSOČTVERCI ZE VZTAHŮ:
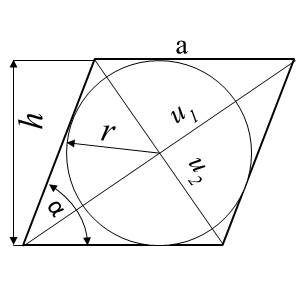 |
 |
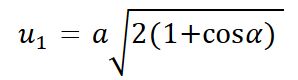 |
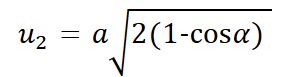 |
KOSOČTVEREC
 |
 |
 |
 |
Definice kosočtverce
Definice kosočtverce
Kosočtverec je rovinný geometrický útvar patřící mezi čtyřúhelníky, který má:
Kosočtverec lze chápat jako speciální případ rovnoběžníku. Pokud mají všechny úhly pravé (90°), stává se z kosočtverce čtverec.
Obsah kosočtverce
Obsah kosočtverce
(S) se může počítat několika způsoby:Druhý vztah vychází z toho, že úhlopříčky kosočtverce se na sebe kolmo půlí. Obsah je tak roven polovině obsahu obdélníku s rozměry úhlopříček.
Obvod kosočtverce
Obvod kosočtverce
(O) se počítá jednoduše podle vzorce O = 4a, kde a je délka strany. Všechny strany kosočtverce jsou stejně dlouhé, proto je jeho obvod čtyřnásobkem jedné strany.Úhlopříčky kosočtverce
Úhlopříčky kosočtverce
Úhlopříčky kosočtverce mají několik důležitých vlastností:Vztah mezi délkou strany a úhlopříčkami je: a = √[(e/2)² + (f/2)²]. Tento vztah se používá při výpočtech v geometrii i technické praxi.
Poloměr kružnice opsané kosočtverci
Poloměr kružnice opsané kosočtverci
Obecně kosočtverec nemá opsanou kružnici, protože součet protilehlých úhlů není 180°. Výjimkou je čtverec, u kterého platí vzorec ro = a√2 / 2.
Poloměr kružnice vepsané kosočtverci
Poloměr kružnice vepsané kosočtverci
Kosočtverec má vepsanou kružnici, protože součet délek jeho protilehlých stran je stejný. Poloměr se dá vyjádřit vztahem:
rv = S / (2a)
kde S je obsah kosočtverce a a délka jeho strany. Vepsaná kružnice se dotýká všech čtyř stran.
Zajímavosti o kosočtverci
Zajímavosti o kosočtverci