Dopocitej.cz - Přejít na úvodní stránku

HRANOL TROJBOKÝ:

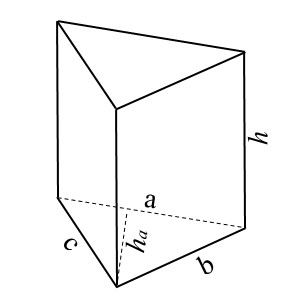
VÝPOČET POVRCHU, POVRCHU PLÁŠTĚ, OBJEMU, STRAN, VÝŠKY A VÝŠKY PODSTAVY TROJBOKÉHO HRANOLU ZE VZTAHŮ:


Geometrické znázornění trojbokého hranolu s vyznačenými délkou hran, výškou podstavy
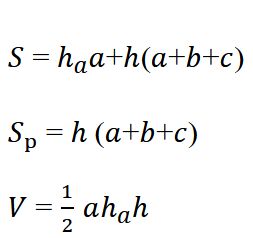Vzorce pro výpočet objemu, povrchu a povrchu plástě trojbokého hranolu
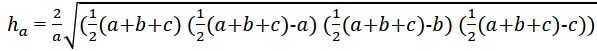Vzorec pro výpočet výšky podstavy na stranu a


TIP: pokud máte zadanou jinou veličinu k výpočtu hranolu můžete ji dopočítat ze vztahů pro obecný trojuhelník

Zadejte jakéchkoliv čtyři veličiny a zvolte všechny jednotky
(pro práci pouze s výpočtem objemu zvolte libovolné tři veličiny ze vztahu)
VÝSLEDKY
Délka nejdelší strany podstavy a =
Délka strany podstavy b =
Délka strany podstavy c =
Výška podstavy na stranu a ha =
Výška hranolu h =
Povrch hranolu S =
Povrch pláště hranolu Sp =
Objem hranolu V =
 a
 b
 c
 ha
 h
 S
 Sp
 V


pozn.: výsledné hodnoty jsou zaokrouhlovány na tři desetinná místa
Definice trojbokého hranolu

Definice trojbokého hranolu

Trojboký hranol je hranaté těleso, které má dvě rovnoběžné podstavy ve tvaru trojúhelníku a tři boční stěny ve tvaru obdélníků (u kolmého hranolu) nebo rovnoběžníků (u šikmého hranolu).

  • Má 5 stěn – 2 trojúhelníkové a 3 obdélníkové nebo rovnoběžníkové,
  • 9 hran a 6 vrcholů.
  • Pokud jsou boční stěny kolmé k podstavám, jedná se o kolmý trojboký hranol.

Trojboký hranol je nejjednodušším typem hranolu a často se používá k modelování střech, ramp nebo hranolových těles v geometrii.

Výška podstavy trojbokého hranolu

Výška podstavy trojbokého hranolu

Výška podstavy (va) je výška trojúhelníku, který tvoří podstavu hranolu. Určuje se jako kolmá vzdálenost od vrcholu trojúhelníku ke straně, která je brána jako základna (a).

  • Pro obecný trojúhelník: va = (2 · Sp) / a
  • Pro rovnostranný trojúhelník: va = (a√3) / 2

Výška podstavy se využívá při výpočtu obsahu trojúhelníkové podstavy a následně objemu hranolu.

Objem trojbokého hranolu

Objem trojbokého hranolu

Objem (V) trojbokého hranolu se vypočítá jako součin obsahu podstavy a výšky hranolu:

  • V = Sp · v

kde Sp je obsah trojúhelníkové podstavy a v je výška hranolu – tedy vzdálenost mezi podstavami.

Pokud má podstava trojúhelník s délkou základny a a výškou va, pak:

  • V = (a · va / 2) · v
Povrch trojbokého hranolu

Povrch trojbokého hranolu

Povrch (S) je součet obsahů všech pěti stěn hranolu – dvou podstav a tří bočních stěn:

  • S = 2 · Sp + Spláště

U kolmého hranolu s trojúhelníkovou podstavou o stranách a, b, c a výšce hranolu v platí:

  • S = 2 · Sp + (a + b + c) · v

Boční stěny jsou zde obdélníky s výškou v a délkami odpovídajícími stranám trojúhelníka.

Povrch pláště trojbokého hranolu

Povrch pláště trojbokého hranolu

Povrch pláště (Spláště) je součet obsahů všech tří bočních stěn hranolu.

Pro kolmý trojboký hranol se stranami podstavy a, b, c a výškou hranolu v platí:

  • Spláště = (a + b + c) · v

Každá boční stěna je obdélník s výškou v a jednou ze stran podstavy. Povrch pláště je tedy celková plocha těchto tří obdélníků.

Úhlopříčka trojbokého hranolu

Úhlopříčka trojbokého hranolu

Úhlopříčka (u) trojbokého hranolu je spojnice dvou protilehlých vrcholů, které neleží v jedné podstavě.

Její délka závisí na tvaru trojúhelníkové podstavy a výšce hranolu. Pokud má podstava hranu a a výšku hranolu v, platí pro kolmý hranol:

  • u = √(a² + v²)

V obecnějším případě se úhlopříčka počítá mezi libovolnými vrcholy pomocí trojrozměrné Pythagorovy věty.

Zajímavosti o trojbokém hranolu

Zajímavosti o trojbokém hranolu

  • Trojboký hranol je nejjednodušší hranol a tvoří základ pro složitější hranoly.
  • Pokud má rovnostrannou trojúhelníkovou podstavu, tvoří tzv. pravidelný trojboký hranol.
  • V praxi má podobu například střechy, nosníku nebo stanového tvaru.
  • Jeho objem a povrch lze snadno vyjádřit pomocí vzorců pro trojúhelník a výšku tělesa.
  • Při kolmém postavení bočních hran se všechny boční stěny stávají obdélníky.